Category: Մաթեմատիկա ա․ բ․

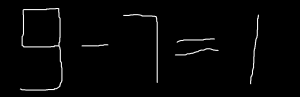
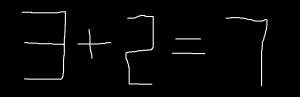
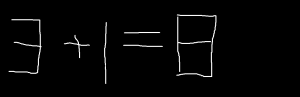Խնդիր 1

Քաղաք Ա-ից գնացքը մեկնեց Քաղաք Բ-ի ուղղությամբ։ 3 ժամ անց, Քաղաք Բ-ից դուրս եկավ  մեկ այլ գնացք, որը շարժվում էր նույն ուղղությամբ։ Առաջին գնացքը շարժվում էր 60 կմ/ժ արագությամբ, իսկ երկրորդը՝ 80 կմ/ժ արագությամբ։ 4 ժամ հետո երկրորդ գնացքը հասավ առաջինին։ Գտիր քաղաքների միջև եղած հեռավորությունը։

100

Խնդիր 2

Ունես՝ 1, 3, 6, 10, 15, 21, … թվային հաջորդականությունը։ Գտի՛ր, ո՞ր թիվն  հաջորդը։

28,36

Խնդիր 3

Պատկերացրեք, որ յուրաքանչյուր թիվ նշանակում է իր տառը՝ հետևյալ ձևով․ 

1 – A

2 – B

3 – C

…

26 — Z: 

Օրինակ՝ 8, 5, 12, 12, 15 նշանակում է HELLO։ Գտե՛ք 19, 5, 3, 18, 5, 20 հաջորդականության գաղտնագիրը։

secret

Խնդիր 4

Գտի՛ր կրկնվող թվանշաններով գրվող այն եռանիշ թվերի քանակը, որոնք   բաժանվում են  3-ի, բայց ոչ՝ 9-ի։

111,222,444,555,777,888

Խնդիր 5

Այսօր հագուստի խանութում գործում է 40% զեղչ։  Աննան ցանկանում է իր համար  գնել ջինսե տաբատ։ Գնապիտակի վրա գրված էր զեղչված գինը՝ 4800 դրամ։ Կարո՞ղ եք գտնել ջինսե տաբատի սկզբնական արժեքը։

8000

Խնդիր 6

Գոշան բնական գիտությունների կաբինետում գտավ 3 կշռաքար և կշեռք։ Պարզվեց, որ՝

• Առաջին կշռաքարը 4 անգամ ծանր է երկրորդից,
• Երրորդ կշռաքարը 3 անգամ ծանր է առաջինից,
• Բոլոր կշռաքարերի ընդհանուր քաշը 340 գրամ է։

Գտեք ամենաթեթև  կշռաքարի քաշը։

Ամենաթեթև՝ 2-20

Խնդիր 7

Շախմատի խմբում կա 11 տղա և 5 աղջիկ։ Ամեն ամիս խմբին միանում է 1 տղա և 3 աղջիկ։ Քանի՞ ամիս անց տղաների և աղջիկների քանակը կլինի հավասար։ 

3 ամսում

Խնդիր 8

Առաջին խողովակը 1 ժամում լցնում է 120 լիտր ջուր, իսկ երկրորդը՝ 140 լիտր։ Քանի՞ լիտր ջուր կլցվի ավազանում 5 ժամում, եթե խողովակները միաժամանակ  բաց լինեն։

1300

Խնդիր 9

Երբ առաջին տակառում  ավելացվեց 34 լիտր գինի, իսկ երկրորդ տակառում՝ 21 լիտր, երկու տակառներում  միասին եղավ 440 լիտր գինի։ Քանի՞ լիտր գինի կար տակառներում  միասին  մինչ ավելացնելը։

385 լիտր

Խնդիր 10

Սեղանի վրա դրված էին 1-ից 9 համարակալված ինը քարտեր: Արմենը, Բաբկենը, Գագիկը և Դավիթը վերցրին երկուական խաղաքարտ: Արմենն ասաց.

«Իմ քարտերի թվերի գումարը 6 է»: Բաբկենն ասաց. «Իմ քարտերի թվերի

տարբերությունը 5 է»: Գագիկն ասաց. «Իմ քարտերի թվերի արտադրյալը 18 է»:

Դավիթն ասաց․ «Իմ քարտերից մեկի թիվը կրկնակի մեծ է մյուսից»: Եթե չորսի

ասածներն էլ ճշմարիտ են, ապա ո՞ր թիվը մնաց սեղանին:

9

Խնդիր 1:
Անուշը ունի 5 տարբեր թիվ: Առաջին թիվը մեծ է երկրորդից, երկրորդը մեծ է երրորդից, իսկ չորրորդ թիվը փոքր է հինգերորդից և մեծ է երրորդից:: Որքա՞ն է ամենափոքր թիվը:

Ամենափոքր թիվը 3-ն է:

Խնդիր2:
Յուրաքանչյուր 10-րդ փուչիկը պայթում է: Եթե դուք փչում եք 100 փուչիկ, ապա քանի՞ փուչիկ կպայթի, մինչև բոլորը պատրաստ լինեն:

10

Խնդիր 3:
Երկու գնացք շարժվում են միմյանց ընդառաջ՝ նույն արագությամբ, 100 կմ հեռավորությամբ: Ծիծեռնակը թռչում է առաջին գնացքից դեպի երկրորդը և վերադառնում  է առաջին գնացքին: Եթե ծիծեռնակը թռչում է 50 կմ/ժ արագությամբ, ապա քանի՞ կիլոմետր է այն անցնում մինչև գնացքները կհանդիպեն:

50 կմ

Խնդիր 4:
Կա 5 քաղաք, որոնք պետք է կապել ճանապարհներով այնպես, որ յուրաքանչյուր քաղաքը կապվի մյուս չորս քաղաքների հետ: Քանի՞ ճանապարհ է անհրաժեշտ:

Խնդիր 5:
Անուշն ունի այգի, որտեղ տարբեր տեսակի ծաղիկներ կան՝ կարմիր, դեղին, և կապույտ: Ամեն օր նա ընտրում է երեք ծաղիկ՝ մեկը ամեն տեսակից: Երրորդ օրը նա տեսնում է, որ իր բոլոր հնարավոր ընտրությունները կատարել է: Քանի՞ ծաղիկ ունի Անուշը:

9

Խնդիր 6

Գծի՛ր 3 ուղիղ և նրանց վրա տեղադրի՛ր 3 կետ այնպես, որ ամեն ուղղի վրա լինի 2 կետ։

1. Նկարներից որո՞ւմ է սպիտակ մասը հավասար մոխրագույն մասին:
(A) (B) (C) (D) (E)
2. Իմ հովանոցի արտաքին կողմի վրա գրված է KANGAROO բառը, ինչպես
ցույց է տրված նկարում: Ներքևում բերված նկարներից որո՞ւմ ցույց
տրված հովանոցն իմը չէ:
(A) (B) (C) (D) (E)
3. Սամվելը նկարում բերված 9 քառակուսիները ներկել է սև, սպիտակ և
մոխրագույն: Ամենաքիչը քանի՞ քառակուսու գույն պետք է նա փոխի
նշված գույներից որևէ մեկով, որպեսզի ընդհանուր կողմ ունեցող
ցանկացած երկու քառակուսի լինեն տարբեր գույների:
(A) 2 (B) 3 (C) 4 (D) 5 (E) 6
4. Կա 10 բադ: Դրանցից 5-ը ձու է ածում ամեն օր, մնացած 5-ը՝ օրումեջ: Քանի՞ ձու կածի
այդ 10 բադը 10 օրում:
(A) 75 (B) 60 (C) 50 (D) 25 (E) 10
5. Նկարում բերված պատկերի յուրաքանչյուր քառակուսու մակերեսը 4 սմ2 է:
Որքա՞ն է հաստ սև գծի երկարությունը:
(A) 16 սմ (B) 18 սմ (C) 20 սմ (D) 21 սմ (E) 23 սմ
6. Կոտորակներից ո՞րն է 2-ից փոքր:
(A) ଵଽ଼ (B) ଶ଴ଽ (C) ଶଵଵ଴ (D) ଶଶଵଵ (E) ଶଷଵଶ
7. Որքա՞ն է կշռում Դիտան:

(A) 2 կգ (B) 3 կգ (C) 4 կգ (D) 5 կգ (E) 6 կգ

8. Վազգենը խոշորացույցով նայում է պատի վրայի պատկերի տարբեր
մասերին (տե՛ս նկարը): Բերված նկարներից ո՞րը նա չի կարող տեսնել:
(A) (B) (C) (D) (E)
9. Բաբկենի այգում յուրաքանչյուր բույս ունի կամ միայն 5 տերև, կամ 2
տերև ու 1 ծաղիկ: Բոլոր բույսերը միասին ունեն 6 ծաղիկ և 42 տերև:
Քանի՞ բույս կա Բաբկենի այգում:
(A) 10 (B) 12 (C) 13 (D) 15 (E) 16
10. Անուշն ունի նույն երկարությամբ չորս թղթե ժապավեն: Նա դրանցից երկուսն իրար է
սոսնձում՝ դնելով ժապավենների ծայրերը մեկը մյուսի վրա 10 սմ վերադրումով, և
ստանում 50 սմ երկարությամբ մեկ ժապավեն (տե՛ս նկարը): Մյուս երկու թղթե
ժապավենով նա ցանկանում է ստանալ 56 սմ երկարությամբ մեկ ժապավեն: Այդ
դեպքում ի՞նչ երկարություն պետք է ունենա վերադրումը:
(A) 4 սմ (B) 6 սմ (C) 8 սմ (D) 10 սմ (E) 12 սմ
4 միավոր գնահատվող խնդիրներ
11. Նկարում բերված պատկերը ստացվել է 6 հատ քառակուսիներից, որոնց
կողմի երկարությունը 1 սմ է: Որքա՞ն է այդ պատկերի պարագիծը:
(A) 9 սմ (B) 10 սմ (C) 11 սմ (D) 12 սմ (E) 13 սմ
12. Ամեն օր Մարիամը գրառում է տվյալ օրվա ամսաթիվն ու ամիսը և գումարում այդ
գրառման թվանշանները: Օրինակ՝ մարտի 26-ը նա գրառում է որպես 26.03 և հաշվում՝
2+6+0+3=11: Ո՞րն է այն ամենամեծ գումարը, որ Մարիամը կստանա տարվա
ընթացքում:
(A) 7 (B) 13 (C) 14 (D) 16 (E) 20
13. Նկարում բերված ܦܥܤܣ ուղղանկյունը բաղկացած է 4 միանման
փոքր ուղղանկյուններից: Դիցուք ܥܤ կողմի երկարությունը 1 սմ
է: Որքա՞ն է ܤܣ կողմի երկարությունը:
(A) 4 սմ (B) 3 սմ (C) 2 սմ (D) 1 սմ (E) 0,5 սմ
14. Բերված պատկերներից ո՞րը ծալելու դեպքում հնարավոր չէ ստանալ բուրգ:
(A) (B) (C) (D) (E)
15. Ջուլհակների փողոցի երկայնքով կողք կողքի կա 9 տուն: Յուրաքանչյուր տանը
բնակվում է ամենաքիչը մեկ մարդ: Ցանկացած երկու հարևան տներում միասին
բնակվում է ամենաշատը վեց մարդ: Ամենաշատը քանի՞ մարդ կարող է ապրել
Ջուլհակների փողոցում:
(A) 23 (B) 25 (C) 27 (D) 29 (E) 31

16. Լուսինեն ու նրա մայրը ծնվել են հունվարին: 2015
թ. մարտի 19-ին Լուսինեն գումարեց
իր ծննդյան թիվը, իր մոր ծննդյան թիվը, իր տարիքը
և իր մոր տարիքը: Ի՞նչ գումար
ստացավ նա:
(A) 4028 (B) 4029 (C) 4030 (D) 4031 (E) 4032
17. Ուղղանկյան մակերեսը 12 սմ2 է: Նրա կողմերի երկարությունները բնական թվեր են:
Այդ դեպքում տվյալ ուղղանկյան պարագիծը կարող է լինել՝
(A) 20 սմ (B) 26 սմ (C) 28 սմ (D) 32 սմ (E) 48 սմ
18. Նկարում ցույց տրված պատկերի 9 հատվածներից յուրաքանչյուրը
պետք է ներկել կամ կարմիր, կամ կապույտ, կամ կանաչ:
Պատկերի յուրաքանչյուր եռանկյան երեք կողմերը պետք է լինեն
տարբեր գույների: Հատվածներից երեքի գույները ցույց են տրված
նկարում: Ի՞նչ գույն կարող է ունենալ
ݔ-ով նշված հատվածը:
(A) միայն կապույտ (B) միայն կանաչ (C) միայն կարմիր
(D) կապույտ, կանաչ կամ կարմիր (E) Հնարավոր չէ նման ձևով ներկել:
19. Տոպրակի մեջ կան 3 կանաչ
և 5 դեղին խնձոր, 7 կանաչ
և 2 դեղին տանձ: Լևոնը
տոպրակի միջից մեկ առ մեկ պատահական կերպով հանում է մրգերը: Ամենաքիչը
քանի՞ միրգ պետք է հանի Լևոնը, որպեսզի վստահ լինի, որ կունենա նույն գույնի
առնվազն մեկ խնձոր
և մեկ տանձ:
(A) 9 (B) 10 (C) 11 (D) 12 (E) 13
20. Ներկայացվում է շախմատի նոր խաղաքար, որը կոչվում է «կենգուրու»: Յուրաքանչյուր
քայլի ընթացքում այն ցատկում է 3 քառակուսի ուղղահայաց
և 1
քառակուսի հորիզոնական ուղղությամբ կամ 3 քառակուսի
հորիզոնական
և 1 քառակուսի ուղղահայաց ուղղությամբ, ինչպես
ցույց է տրված նկարում: Ամենաքիչը քանի՞ ցատկ պետք է կատարի
«կենգուրու» խաղաքարը, որպեսզի այն քառակուսուց, որում նա
գտնվում է նկարում, հայտնվի A-ով նշված քառակուսում:
(A) 2 (B) 3 (C) 4 (D) 5 (E) 6
5 միավոր գնահատվող խնդիրներ
21. Նկարում բերված գումարման մեջ նույն տառերին համապատասխանում են
նույն թվանշանները, տարբեր տառերին՝ տարբեր թվանշաններ: Ո՞ր
թվանշանն է համապատասխանում X տառին:
(A) 2 (B) 3 (C) 4 (D) 5 (E) 6
22. Գոհարը գնեց երեք խաղալիք: Առաջին խաղալիքի համար նա վճարեց իր ունեցած
ամբողջ գումարի կեսը
և ևս 100 դրամ: Երկրորդ խաղալիքի համար նա վճարեց մնացած
գումարի կեսը
և ևս 200 դրամ: Երրորդ խաղալիքի համար նա վճարեց մնացած գումարի
կեսը
և ևս 300 դրամ՝ այդպիսով ծախսելով իր ունեցած ամբողջ գումարը: Գոհարը քանի՞
դրամ ուներ սկզբում:
(A) 3600 դրամ (B) 4500 դրամ (C) 3400 դրամ (D) 6500 դրամ (E) 10000 դրամ
23. Կարինեն ցանկանում է թուղթը ծալելով ստանալ խորանարդ: Նա 6
քառակուսու փոխարեն թղթի վրա սխալմամբ գծել է 7 քառակուսի
(տե՛ս նկարը): Կարինեն ո՞ր քառակուսին պետք է ջնջի, որպեսզի

մնացած իրար կպած քառակուսիներից ստանա խորանարդ:
(A) միայն համար 4-
ը (B) միայն համար 7-
ը (C) համար 3-
ը կամ 4-
ը
(D) համար 3-
ը կամ 7-
ը (E) համար 3-
ը, 4-
ը կամ 7-
ը
24. 100 թիվը բազմապատկում են 2-ով կամ 3-ով, ապա արդյունքին գումարում 1 կամ 2
և
այնուհետև ստացված արդյունքը բաժանում 3-
ի կամ 4-
ի: Վերջնական արդյունքը
բնական թիվ է: Ո՞րն է այդ թիվը:
(A) 50 (B) 51 (C) 67 (D) 68
(E) Հնարավոր է ստանալ մեկից ավելի արդյունք:
25.
ܥ ,ܤ ,ܣ
և
ܦ թվանշաններով կազմված քառանիշ թիվը կարելի է ներկայացնել ܦܥܤܣ തതതതതതതത
տեսքով: ܦܥܤܣ തതതതതതതത քառանիշ թվի
ܥ ,ܤ ,ܣ
և
ܦ թվանշանները աճում են ձախից աջ: Որքա՞ն է
երկնիշ ܦܤതതതത և ܥܣതതതത թվերի ܦܤതതതത– ܥܣതതതത տարբերության հնարավոր առավելագույն արժեքը:
(A) 86 (B) 61 (C) 56 (D) 50 (E) 16
26. Արեգը խորանարդի յուրաքանչյուր նիստի վրա գրեց թվեր, այնուհետև յուրաքանչյուր
գագաթի համար գումարեց այն երեք նիստերի վրա գրված թվերը,
որոնց վրա կա տվյալ գագաթը: Օրինակ՝
ܤ գագաթի համար նա
ܨܧܣܤ ,ܣܦܥܤ է գումարել
և ܥܩܨܤ նիստերի վրա գրված թվերը: ܥ ,ܦ
և
ܧ
գագաթների համար Արեգը ստացավ համապատասխանաբար 14, 16
և
24 թվերը: Ի՞նչ թիվ նա կստանա
ܨ գագաթի համար:
(A) 15 (B) 19 (C) 22 (D) 24 (E) 26
27. Գնացքն ունի 12 վագոն: Յուրաքանչյուր վագոն ունի խցիկների միևնույն քանակը:
Տիգրանը ճանապարհորդում է գնացքի սկզբից հաշված 18-րդ խցիկում, որը գտնվում է
3-րդ վագոնում: Լիլիթը նստել է գնացքի սկզբից հաշված 50-րդ խցիկում, որը գտնվում է
7-րդ վագոնում: Քանի՞ խցիկ կա յուրաքանչյուր վագոնում:
(A) 7 (B) 8 (C) 9 (D) 10 (E) 12
28. Քանի՞ տարբեր եղանակով կարելի է տեղավորել 3 միանման կենգուրուները նկարում
պատկերված վանդակներից երեքում այնպես, որ ոչ մի երկու կենգուրու չլինի հարևան
վանդակներում:
(A) 7 (B) 8 (C) 9 (D) 10 (E) 11
29. Գծի վրա նշված է չորս կետ: Դրանց միջև հեռավորությունները, ըստ աճման կարգի,
հետևյալն են՝ 2, 3, ݇, 11, 12, 14: Ինչի՞ է հավասար ݇-ն:
(A) 9 (B) 8 (C) 7 (D) 6 (E) 5
30. Բագրատը կառուցեց 4 սմ կող ունեցող խորանարդ՝ օգտագործելով խորանարդիկներ,
որոնց կողը հավասար էր 1 սմ-ի: Ստացված խորանարդի նիստերից երեքը նա ներկեց
կարմիր, մնացած երեքը՝ կապույտ: Արդյունքում պարզվեց, որ խորանարդիկներից ոչ
մեկը չուներ 3 կարմիր նիստ: Խորանարդիկներից քանի՞սն ունեին և՛ կարմիր, և՛
կապույտ նիստեր:
(A) 0 (B) 8 (C) 12 (D) 24 (E) 32

1. Եթե
▲ +
▲ + 6 =
▲ +
▲ +
▲ +
▲, ապա ի՞նչ թիվ է թաքնված
▲ նշանի տակ:
(A) 2 (B) 3 (C) 4 (D) 5 (E) 6
2. Երբ 4 թիվը դրված է երկու հայելիների մոտ, դրանցում
երկու անգամ անդրադառնալուց հետո ստացվում են
նկարում բերված պատկերները։ Ո՞ր պատկերը կլինի
հարցական նշանի տեղում, եթե նույն 4-
ի փոխարեն
տեղադրենք 5 թիվը։
(A) (B) (C) (D) (E)
3. Փոքրիկ Կենգուն գազանանոցից գնում է դպրոց, ճանապարհին հաշվելով բոլոր
ծաղիկները։ Հետևյալ թվերից ո՞րը նա չի կարող ստանալ արդյունքում, եթե նա շարժվում
է միայն դպրոցի ուղղությամբ։
(A) 9 (B) 10 (C) 11 (D) 12 (E) 13
4. Սանդուղքն ունի 21 աստիճան։ Աշոտը
և Միքայելը հաշվում են աստիճանները՝ մեկը
շարժվելով վերևից ներքև, մյուսը՝ ներքևից վերև։ Նրանք հանդիպեցին Աշոտի
հաշվարկով 10-րդ աստիճանի վրա։ Միքայելի հաշվարկով ո՞ր աստիճանի վրա նրանք
հանդիպեցին։
(A) 13 (B) 14 (C) 11 (D) 12 (E) 10
5. Աննան միացրեց յուրաքանչյուր վերևի կետը յուրաքանչյուր ներքևի
կետին։ Քանի՞ հատված գծեց Աննան։
(A) 20 (B) 25 (C) 30 (D) 35 (E) 40
6. Արկղում դրված է 7 հավասար ուղղանկյուն։ Սահեցնելով հնարավոր է
տեղաշարժել այդ ուղղանկյուններն այնպես, որ արկղում տեղ լինի ևս
մեկ նույնանման ուղղանկյան համար։ Առնվազն քանի՞ ուղղանկյուն
պետք է տեղաշարժել։
(A) 1 (B) 2 (C) 3 (D) 4 (E) 5

7. Ճանճը ունի 6 ոտք, իսկ սարդը՝ 8 ոտք։ 2 ճանճը
և 3 սարդը ունեն նույնքան ոտք, որքան 10
թռչունը
և
(A) 2 կատուն (B) 3 կատուն (C) 4 կատուն (D) 5 կատուն (E) 6 կատուն
8. Քառակուսի թղթի մի կողմը մոխրագույն է,
մյուսը՝ սպիտակ։ Աննան բաժանել է այն
ինը հավասար քառակուսիների (տե՛ս նկ. 1)։
Ո՞ր գծերով նա պետք է կտրի թուղթը,
որպեսզի կարողանա այն ծալել այնպես,
ինչպես ցույց է տրված նկար 2-ում։
(A) 1, 3, 5
և 7 (B) 2, 4, 6
և 8 (C) 2, 3, 5
և 6 (D) 3, 4, 6
և 7 (E) 1, 4, 5
և 8
9. Ինչի՞ է հավասար նկարում բերված պատկերի պարագիծը, եթե
բոլոր հարևան կողմերը միմյանց ուղղահայաց են:
(A) 3×5 + 4×2 (B) 3×5 + 8×2 (C) 6×5 + 4×2
(D) 6×5 + 6×2 (E) 6×5 + 8×2
10. Նկարում բերված են սեղանի վրա դրված հինգ հանգույցի պատկերները վերևից։
Իրականում դրանցից միայն մեկն է հանգույց, մնացածները ուղղակի ունեն հանգույցի
տեսք։ Դրանցից ո՞րն է հանգույցը։
(A) (B) (C) (D) (E)
4 միավոր գնահատվող խնդիրներ
11. Տրված արտահայտություններից որի՞ արժեքն է տարբերվում մնացած
արտահայտությունների արժեքներից։
A) 20 × 10 + 20 × 10 B) 20 ÷ 10 × 20 ×10 C) 20 × 10 × 20 ÷ 10
D) 20 × 10 + 10 × 20 E) 20 ÷ 10 × 20 +10
12. Եթե պատկերը պտտենք կես շրջանագծով F կետի շուրջ, կստանանք
(A) (B) (C) (D) (E)
13. Մրջյունը շարժվում է վանդակավոր տետրի գծերով։ Նա սկսում
և
ավարտում է շարժումը նույն կետում։ Ոչ մի ուրիշ կետով մրջյունը
երկու անգամ չի անցնում։ Նա պարտադիր պետք է շարժվի նշված
հատվածներով։ Ամենաքիչը քանի՞ վանդակ կարող է գտնվել
մրջույնի անցած հատվածներով սահմանափակված մասում։
(A) 8 (B) 9 (C) 10 (D) 11 (E) 13
14. Բաբկենը մտքում պահեց մի թիվ, բաժանեց այն 7-
ի, ստացվածին գումարեց 7
և
վերջապես ստացված արդյունքը բազմապատկեց 7-ով։ Այդպես նա ստացավ 777։ Ո՞ր
թիվն էր մտապահել Բաբկենը:
(A) 7 (B) 111 (C) 722 (D) 567 (E) 728

15. 1, 4, 7, 10
և 13 թվերը պետք է գրել նկարի վանդակներում այնպես, որ
հորիզոնական վանդակներում գրված թվերի գումարը հավասար լինի
ուղղահայաց վանդակներում գրված թվերի գումարին։ Ինչքա՞ն է այդ
գումարի հնարավոր ամենամեծ արժեքը։
(A) 18 (B) 20 (C) 21 (D) 22 (E) 24
16. 60 էջանոց գիրքը ստացվում է 15 թերթն իրար վրա դնելուց
և ծալելուց հետո։ Դիցուք, 7-
րդ էջը պարունակող թերթը բացակայում է։ Ուրիշ ո՞ր էջերն են նաև բացակայում այդ
գրքում:
(A) 8, 9
և 10 (B) 8, 42
և 43 (C) 8, 48
և 49 (D) 8, 52
և 53 (E) 8, 53
և 54
17. Օգտվելով նկարից՝ կարող ենք ասել, որ 1 + 3 + 5 + 7 = 4 x 4։ Ինչի՞ է
հավասար 1 + 3 + 5 + 7 + … + 17 + 19 + 21։
(A) 10×10 (B) 11×11 (C) 12×12 (D) 13×13 (E) 14×14
18. Անուշը նկարել է 5 ծաղկաթերթով ծաղիկ։ Նա ուզում է ներկել
ծաղիկը
և ունի միայն 2 գույն՝ մոխրագույն
և սպիտակ:
Համարենք, որ նկարում պատկերված ծաղիկները
գունավորված են մեկ եղանակով։ Քանի՞ տարբեր ծաղիկ
կարող է ստանալ Անուշը, եթե յուրաքանչյուր ծաղկաթերթը
ներկի այս երկու գույներից միայն մեկով։
(A) 6 (B) 7 (C) 8 (D) 9 (E) 10
19. Քառակուսու ո՞ր մասն է կազմում ստվերագծված մասը։
(A) 1
3
(B) 1
4
(C) 1
5
(D) 3
8
(E) 2
9
20. Երեք միատեսակ զառ սոսնձված են իրար, ինչպես ցույց է տրված նկարում։ Զառի
հակադիր կողմերի վրայի կետիկների ընդհանուր քանակը միշտ
հավասար է 7-ի։ Ընդհանուր քանի՞ կետ կա սոսնձված կողմերի վրա։
(A) 12 (B) 13 (C) 14 (D) 15 (E) 16
5 միավոր գնահատվող խնդիրներ
21. Նկարում պատկերված սարքը հավասարակշռված է։ Հորիզոնական ձողերի
և ուղղաձիգ
լարերի կշիռը կարելի է անտեսել։ Մարմինների ընդհանուր
զանգվածը 112 գրամ է։ Ինչքա՞ն է աստղի զանգվածը։
(A) 6 (B) 7 (C) 12 (D) 16 (E) չենք կարող որոշել
22. Պիցցայի խանութում վաճառվող պիցցաների բոլոր
տեսակները պարունակում են պանիր
և պոմիդոր։ Դրանց վրա
ավելացվում են ներքոհիշյալ լրացումներից մեկը կամ երկուսը. եգիպտացորեն, երշիկ,
սունկ, բաստուրմա։ Պիցցաները կարող են լինել երեք տարբեր չափերի՝ փոքր, միջին
և
մեծ։ Քանի՞ տարբեր տեսակի պիցցա կարելի է գնել խանութում։
(A) 30 (B) 12 (C) 18 (D) 48 (E) 72
23. Որպեսզի որոշեն, թե ում կհասնի Լիլիթի ծծնդյան տորթի վերջին կտորը, Լիլիթը,
Սեդան, Հրանտը, Պետրոսն ու Արմենը նստում են շրջանագծով ժամսլաքի ուղղությամբ՝
նշված հաջորդականությամբ: Նրանք սկսում են հաշվել «Կեն-գու-րու-դուրս-գնա-դու»
ժամսլաքի ուղղությամբ։ Այն երեխան, որին հաշվում
և անվանում են «դու», դուրս է
գալիս խաղից: Խաղը շարունակվում է հաջորդից այնքան ժամանակ, մինչև մնում է մեկ

հոգի: Լիլիթը որոշում է, թե ումից են սկսում հաշվարկը։ Ո՞ւմ պետք է նա ընտրի,
որպեսզի տորթի վերջին կտորը հասնի իր լավագույն ընկերոջը՝ Արմենին։
(A) Լիլիթ (B) Սեդա (C) Հրանտ (D) Պետրոս (E) Արմեն

24. Եթե PPQ Q RQ Q   5 հավասարման մեջ P, Q
և R տառերը համապատասխանում են
տարբեր թվանշանների ( PQ -ն
P
և
Q թվանշաններից բաղկացած թիվ է), ապա P+Q+R =
(A) 13 (B) 15 (C) 16 (D) 17 (E) 20